
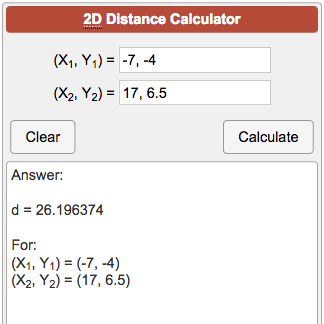
This is because we are defining the distance between two points in the Pythagorean way of geometry, as the size of the hypotenuse for a triangle in which the vertices are defined by the points given. Use the distance calculator to check your results. You bet it does! As your intuition is correctly telling you, the square root of the sum of squares resembles a lot that of the Pythagorean theorem. Calculation assumes that the Earth is a sphere with a radius of 6378km. \ĭoes this have to do anything with Pythagoras Calculates the distance and azimuth between two places from latitudes and longitudes.
Distance math calculator how to#
Assume that we have two points \((x_1, y_1)\) and \((x_2, y_2)\), then the distance formula is computed as follows: Even so, understanding the basics behind the concept and comprehending how the math works is vital to ensuring that you understand exactly how to calculate.

This calculator is based on the distance for the Euclidean geometry. And all of those geometries, including the Euclidean geometry, all define distances that are logical and consistent, and hold all the properties that are expected for a distance. Indeed, different types of geometry can use different types of distances. Although, it is not a static or universal concept, as there many potential measures of "distance" in Math.
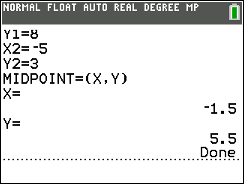
The distance between two points in the Euclidean plane is one of basic concepts in Geometry.


 0 kommentar(er)
0 kommentar(er)
